Mesh¶
Open3D has a data structure for 3D triangle meshes called TriangleMesh. The code below shows how to read a triangle mesh from a ply file and print its vertices and triangles.
[2]:
print("Testing mesh in Open3D...")
mesh = o3dtut.get_knot_mesh()
print(mesh)
print('Vertices:')
print(np.asarray(mesh.vertices))
print('Triangles:')
print(np.asarray(mesh.triangles))
Testing mesh in Open3D...
TriangleMesh with 1440 points and 2880 triangles.
Vertices:
[[ 4.51268387 28.68865967 -76.55680847]
[ 7.63622284 35.52046967 -69.78063965]
[ 6.21986008 44.22465134 -64.82303619]
...
[-22.12651634 31.28466606 -87.37570953]
[-13.91188431 25.4865818 -86.25827026]
[ -5.27768707 23.36245346 -81.43279266]]
Triangles:
[[ 0 12 13]
[ 0 13 1]
[ 1 13 14]
...
[1438 11 1439]
[1439 11 0]
[1439 0 1428]]
The TriangleMesh class has a few data fields such as vertices and triangles. Open3D provides direct memory access to these fields via numpy.
Visualize a 3D mesh¶
[3]:
print("Try to render a mesh with normals (exist: " +
str(mesh.has_vertex_normals()) + ") and colors (exist: " +
str(mesh.has_vertex_colors()) + ")")
o3d.visualization.draw_geometries([mesh])
print("A mesh with no normals and no colors does not look good.")
Try to render a mesh with normals (exist: True) and colors (exist: False)

A mesh with no normals and no colors does not look good.
You can rotate and move the mesh but it is painted with uniform gray color and does not look “3d”. The reason is that the current mesh does not have normals for vertices or faces. So uniform color shading is used instead of a more sophisticated Phong shading.
Surface normal estimation¶
Let’s draw the mesh with surface normals.
[4]:
print("Computing normal and rendering it.")
mesh.compute_vertex_normals()
print(np.asarray(mesh.triangle_normals))
o3d.visualization.draw_geometries([mesh])
Computing normal and rendering it.
[[ 0.79164373 -0.53951444 0.28674793]
[ 0.8319824 -0.53303008 0.15389681]
[ 0.83488162 -0.09250101 0.54260136]
...
[ 0.16269924 -0.76215917 -0.6266118 ]
[ 0.52755226 -0.83707495 -0.14489352]
[ 0.56778973 -0.76467734 -0.30476777]]

It uses compute_vertex_normals and paint_uniform_color which are member functions of mesh.
Crop mesh¶
We remove half of the surface by directly operating on the triangle and triangle_normals data fields of the mesh. This is done via numpy.
[5]:
print("We make a partial mesh of only the first half triangles.")
mesh1 = copy.deepcopy(mesh)
mesh1.triangles = o3d.utility.Vector3iVector(
np.asarray(mesh1.triangles)[:len(mesh1.triangles) // 2, :])
mesh1.triangle_normals = o3d.utility.Vector3dVector(
np.asarray(mesh1.triangle_normals)[:len(mesh1.triangle_normals) // 2, :])
print(mesh1.triangles)
o3d.visualization.draw_geometries([mesh1])
We make a partial mesh of only the first half triangles.
std::vector<Eigen::Vector3i> with 1440 elements.
Use numpy.asarray() to access data.

Paint mesh¶
paint_uniform_color paints the mesh with a uniform color. The color is in RGB space, [0, 1] range.
[6]:
print("Painting the mesh")
mesh1.paint_uniform_color([1, 0.706, 0])
o3d.visualization.draw_geometries([mesh1])
Painting the mesh

Mesh properties¶
A triangle mesh has several properties that can be tested with Open3D. One important property is the manifold property, where we can test the triangle mesh if it is edge manifold is_edge_manifold and if it is is_vertex_manifold. A triangle mesh is edge manifold, if each edge is bounding either one or two triangles. The function is_edge_manifold has the bool parameter allow_boundary_edges that defines if boundary edges should be allowed. Further, a triangle mesh is vertex
manifold if the star of the vertex is edge‐manifold and edge‐connected, e.g., two or more faces connected only by a vertex and not by an edge.
Another property is the test of self-intersection. The function is_self_intersecting returns True if there exists a triangle in the mesh that is intersecting another mesh. A watertight mesh can be defined as a mesh that is edge manifold, vertex manifold and not self intersecting. The function is_watertight implements this check in Open3D.
We also can test the triangle mesh, if it is orientable, i.e. the triangles can be oriented in such a way that all normals point towards the outside. The corresponding function in Open3D is called is_orientable.
The code below tests a number of triangle meshes against those properties and visualizes the results. Non-manifold edges are shown in red, boundary edges in green, non-manifold vertices are visualized as green points, and self-intersecting triangles are shown in pink.
[7]:
def check_properties(name, mesh):
mesh.compute_vertex_normals()
edge_manifold = mesh.is_edge_manifold(allow_boundary_edges=True)
edge_manifold_boundary = mesh.is_edge_manifold(allow_boundary_edges=False)
vertex_manifold = mesh.is_vertex_manifold()
self_intersecting = mesh.is_self_intersecting()
watertight = mesh.is_watertight()
orientable = mesh.is_orientable()
print(name)
print(f" edge_manifold: {edge_manifold}")
print(f" edge_manifold_boundary: {edge_manifold_boundary}")
print(f" vertex_manifold: {vertex_manifold}")
print(f" self_intersecting: {self_intersecting}")
print(f" watertight: {watertight}")
print(f" orientable: {orientable}")
geoms = [mesh]
if not edge_manifold:
edges = mesh.get_non_manifold_edges(allow_boundary_edges=True)
geoms.append(o3dtut.edges_to_lineset(mesh, edges, (1, 0, 0)))
if not edge_manifold_boundary:
edges = mesh.get_non_manifold_edges(allow_boundary_edges=False)
geoms.append(o3dtut.edges_to_lineset(mesh, edges, (0, 1, 0)))
if not vertex_manifold:
verts = np.asarray(mesh.get_non_manifold_vertices())
pcl = o3d.geometry.PointCloud(
points=o3d.utility.Vector3dVector(np.asarray(mesh.vertices)[verts]))
pcl.paint_uniform_color((0, 0, 1))
geoms.append(pcl)
if self_intersecting:
intersecting_triangles = np.asarray(
mesh.get_self_intersecting_triangles())
intersecting_triangles = intersecting_triangles[0:1]
intersecting_triangles = np.unique(intersecting_triangles)
print(" # visualize self-intersecting triangles")
triangles = np.asarray(mesh.triangles)[intersecting_triangles]
edges = [
np.vstack((triangles[:, i], triangles[:, j]))
for i, j in [(0, 1), (1, 2), (2, 0)]
]
edges = np.hstack(edges).T
edges = o3d.utility.Vector2iVector(edges)
geoms.append(o3dtut.edges_to_lineset(mesh, edges, (1, 0, 1)))
o3d.visualization.draw_geometries(geoms, mesh_show_back_face=True)
[8]:
check_properties('Knot', o3dtut.get_knot_mesh())
check_properties('Moebius', o3d.geometry.TriangleMesh.create_moebius(twists=1))
check_properties("non-manifold edge", o3dtut.get_non_manifold_edge_mesh())
check_properties("non-manifold vertex", o3dtut.get_non_manifold_vertex_mesh())
check_properties("open box", o3dtut.get_open_box_mesh())
check_properties("intersecting_boxes", o3dtut.get_intersecting_boxes_mesh())
Knot
edge_manifold: True
edge_manifold_boundary: True
vertex_manifold: True
self_intersecting: False
watertight: True
orientable: True

Moebius
edge_manifold: True
edge_manifold_boundary: False
vertex_manifold: True
self_intersecting: False
watertight: False
orientable: False

non-manifold edge
edge_manifold: False
edge_manifold_boundary: False
vertex_manifold: True
self_intersecting: False
watertight: False
orientable: True

non-manifold vertex
edge_manifold: True
edge_manifold_boundary: True
vertex_manifold: False
self_intersecting: False
watertight: False
orientable: True

open box
edge_manifold: True
edge_manifold_boundary: False
vertex_manifold: True
self_intersecting: False
watertight: False
orientable: True

intersecting_boxes
edge_manifold: True
edge_manifold_boundary: True
vertex_manifold: True
self_intersecting: True
watertight: False
orientable: True
# visualize self-intersecting triangles

Mesh filtering¶
Open3D contains a number of methods to filter meshes. In the following we show the implemented filters to smooth noisy triangle meshes.
Average filter¶
The simplest filter is the average filter. A given vertex \(v_i\) is given by the average of the adjacent vertices \(\mathcal{N}\)
This filter can be used to denoise meshes as demonstrated in the code below. The parameter number_of_iterations in the function filter_smooth_simple defines the how often the filter is applied to the mesh.
[9]:
print('create noisy mesh')
mesh_in = o3dtut.get_knot_mesh()
vertices = np.asarray(mesh_in.vertices)
noise = 5
vertices += np.random.uniform(0, noise, size=vertices.shape)
mesh_in.vertices = o3d.utility.Vector3dVector(vertices)
mesh_in.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh_in])
print('filter with average with 1 iteration')
mesh_out = mesh_in.filter_smooth_simple(number_of_iterations=1)
mesh_out.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh_out])
print('filter with average with 5 iterations')
mesh_out = mesh_in.filter_smooth_simple(number_of_iterations=5)
mesh_out.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh_out])
create noisy mesh

filter with average with 1 iteration

filter with average with 5 iterations

Laplacian¶
Another important mesh filter is the Laplacian defined as
where \(\lambda\) is the strength of the filter and \(w_n\) are normalized weights that relate to the distance of the neighboring vertices. The filter is implemented in filter_smooth_laplacian and has the parameters number_of_iterations and lambda.
[10]:
print('filter with Laplacian with 10 iterations')
mesh_out = mesh_in.filter_smooth_laplacian(number_of_iterations=10)
mesh_out.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh_out])
print('filter with Laplacian with 50 iterations')
mesh_out = mesh_in.filter_smooth_laplacian(number_of_iterations=50)
mesh_out.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh_out])
filter with Laplacian with 10 iterations

filter with Laplacian with 50 iterations

Taubin filter¶
The problem with the average and Laplacian filter is that they lead to a shrinkage of the triangle mesh. [Taubin1995] showed that the application of two Laplacian filters with different \(\lambda\) parameters can prevent the mesh shrinkage. The filter is implemented in filter_smooth_taubin.
[11]:
print('filter with Taubin with 10 iterations')
mesh_out = mesh_in.filter_smooth_taubin(number_of_iterations=10)
mesh_out.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh_out])
print('filter with Taubin with 100 iterations')
mesh_out = mesh_in.filter_smooth_taubin(number_of_iterations=100)
mesh_out.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh_out])
filter with Taubin with 10 iterations

filter with Taubin with 100 iterations

Sampling¶
Open3D includes functions to sample point clouds from a triangle mesh. The simplest method is sample_points_uniformly that uniformly samples points from the 3D surface based on the triangle area. The parameter number_of_points defines how many points are sampled from the triangle surface.
[12]:
mesh = o3d.geometry.TriangleMesh.create_sphere()
mesh.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh])
pcd = mesh.sample_points_uniformly(number_of_points=500)
o3d.visualization.draw_geometries([pcd])


[13]:
mesh = o3dtut.get_bunny_mesh()
mesh.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh])
pcd = mesh.sample_points_uniformly(number_of_points=500)
o3d.visualization.draw_geometries([pcd])

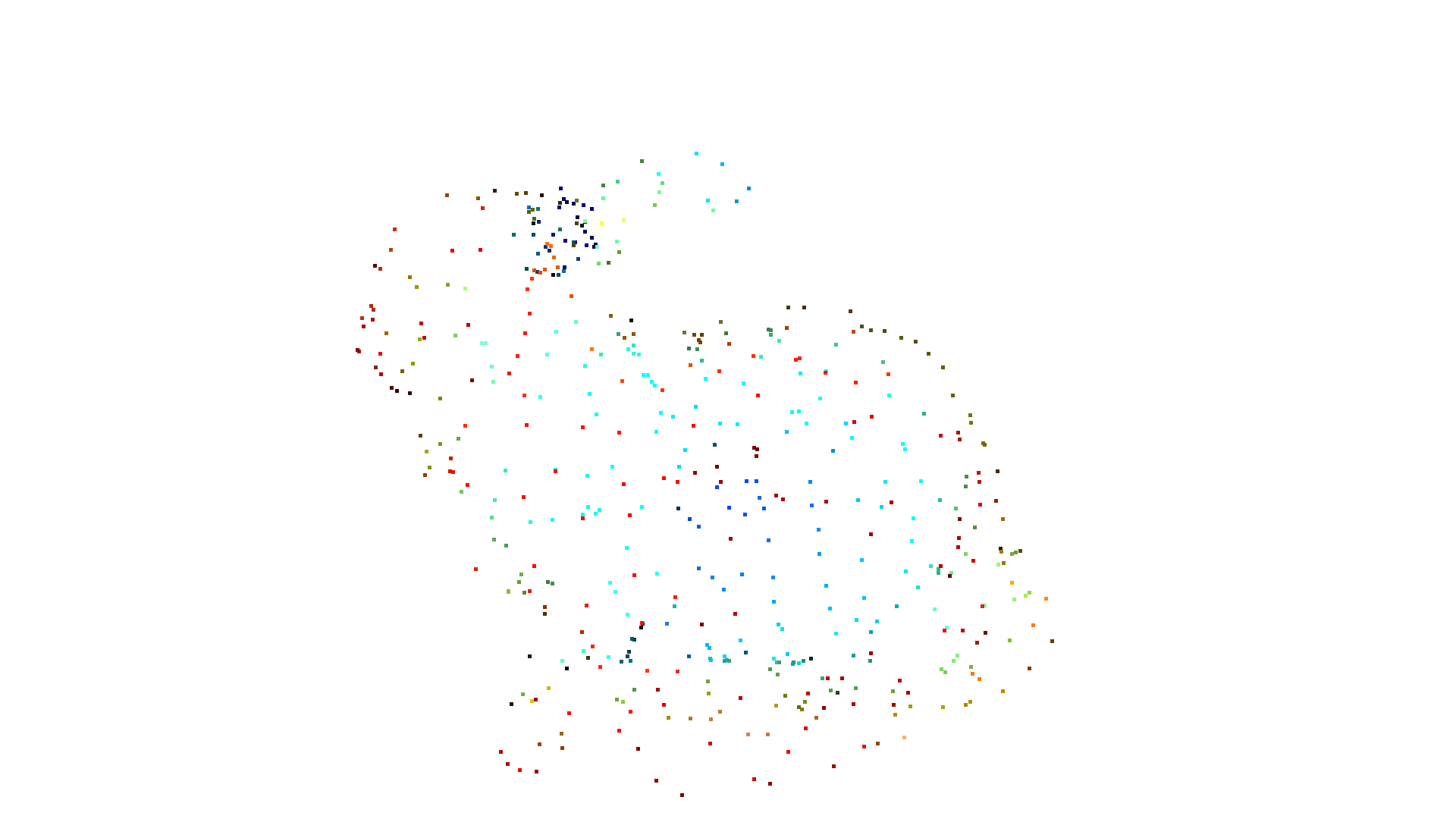
Uniform sampling can yield clusters of points on the surface, while a method called Poisson disk sampling can evenly distribute the points on the surface. The method sample_points_poisson_disk implements sample elimination. It starts with a sampled point cloud and removes points to satisfy the sampling criterion. The method supports two options to provide the initial point cloud:
Default via the parameter
init_factor: The method first samples uniformly a point cloud from the mesh withinit_factorxnumber_of_pointsand uses this for the elimination.One can provide a point cloud and pass it to the
sample_points_poisson_diskmethod. Then, this point cloud is used for elimination.
[14]:
mesh = o3d.geometry.TriangleMesh.create_sphere()
pcd = mesh.sample_points_poisson_disk(number_of_points=500, init_factor=5)
o3d.visualization.draw_geometries([pcd])
pcd = mesh.sample_points_uniformly(number_of_points=2500)
pcd = mesh.sample_points_poisson_disk(number_of_points=500, pcl=pcd)
o3d.visualization.draw_geometries([pcd])


[15]:
mesh = o3dtut.get_bunny_mesh()
pcd = mesh.sample_points_poisson_disk(number_of_points=500, init_factor=5)
o3d.visualization.draw_geometries([pcd])
pcd = mesh.sample_points_uniformly(number_of_points=2500)
pcd = mesh.sample_points_poisson_disk(number_of_points=500, pcl=pcd)
o3d.visualization.draw_geometries([pcd])
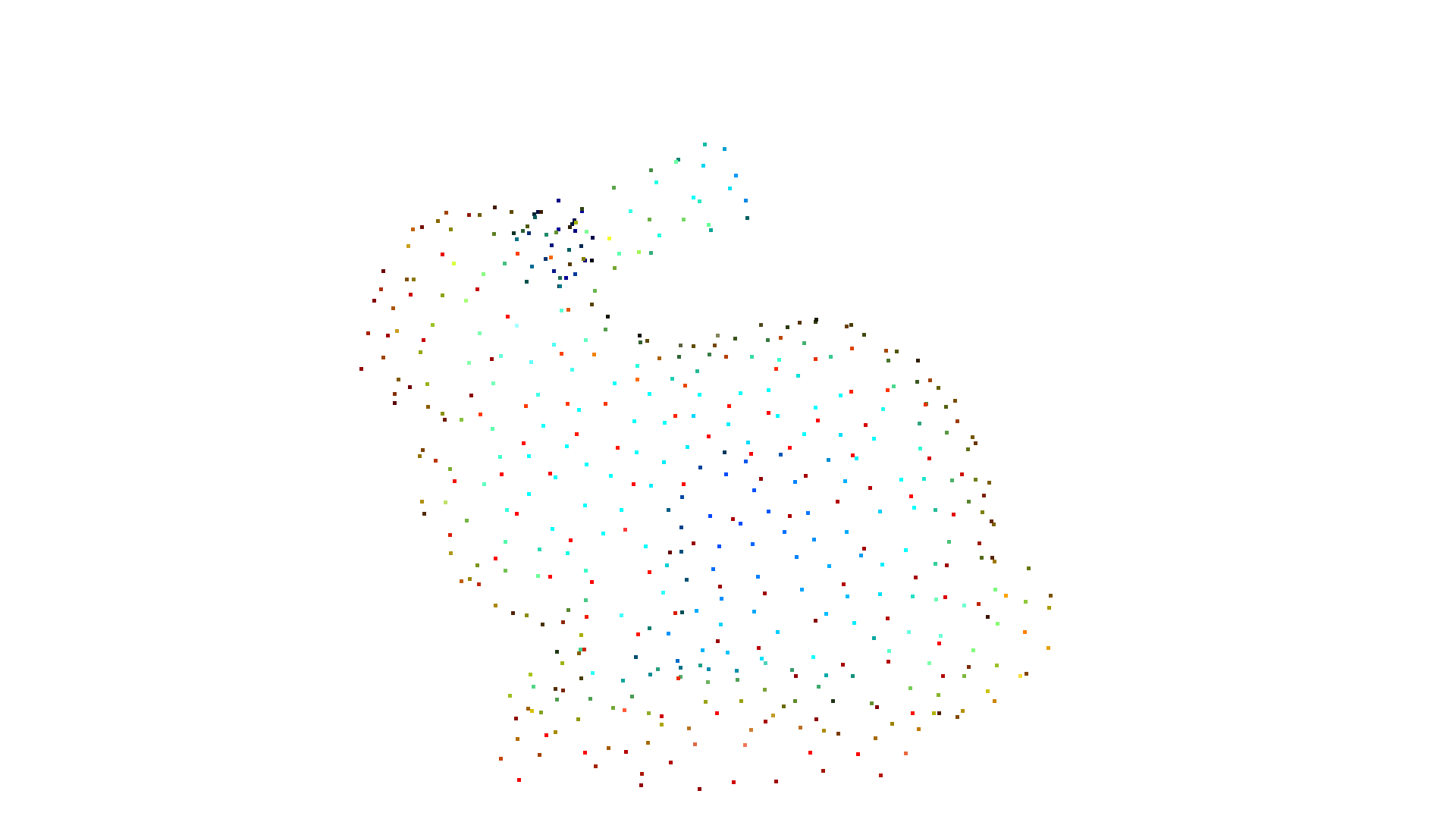
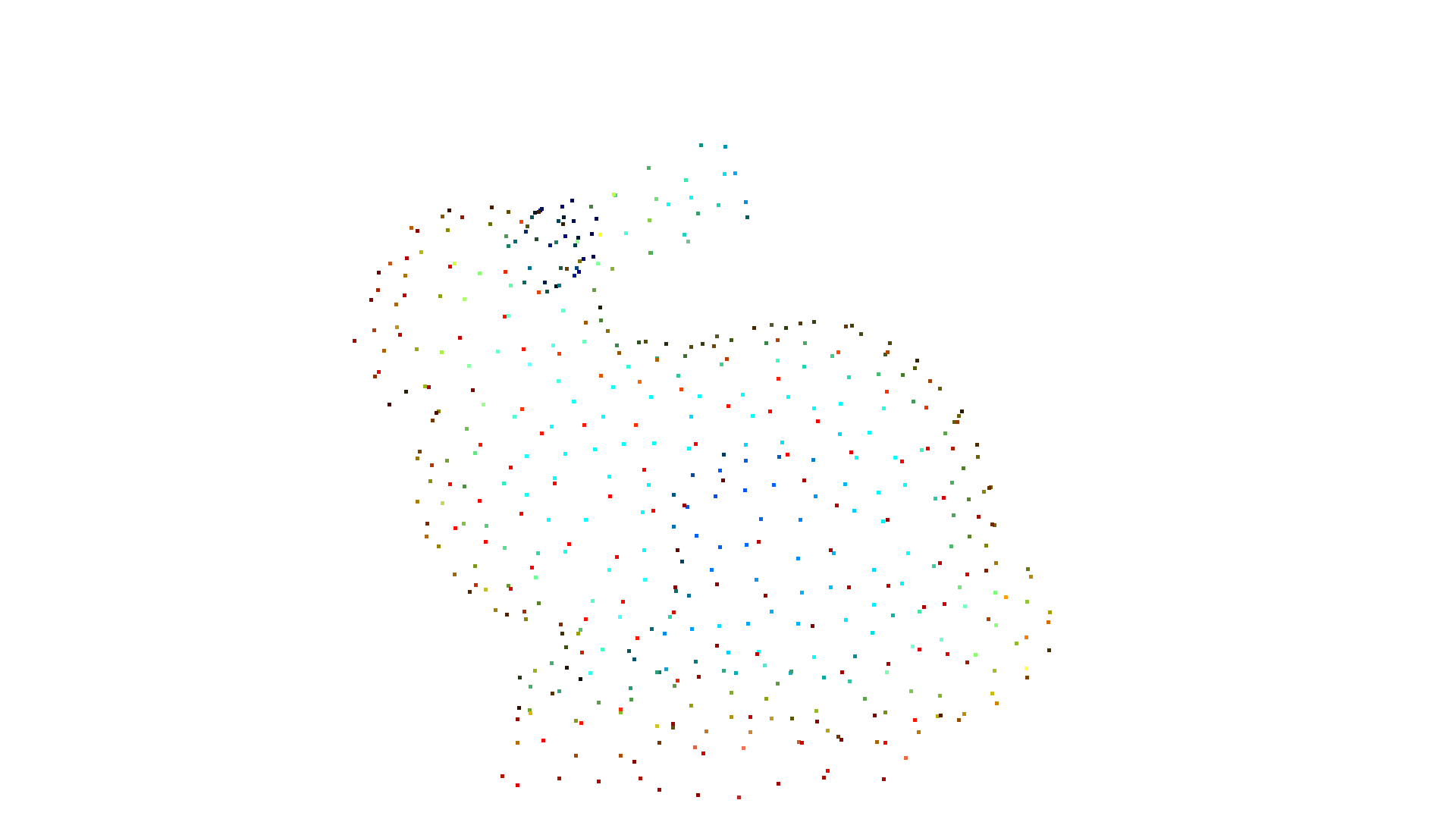
Mesh subdivision¶
In mesh subdivision we divide each triangle into a number of smaller triangles. In the simplest case, we compute the midpoint of each side per triangle and divide the triangle into four smaller triangles. This is implemented in the subdivide_midpoint function. The 3D surface and area stays the same, but the number of vertices and triangles increases. The parameter number_of_iterations defines how many times this process should be repeated.
[16]:
mesh = o3d.geometry.TriangleMesh.create_box()
mesh.compute_vertex_normals()
print(
f'The mesh has {len(mesh.vertices)} vertices and {len(mesh.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh], zoom=0.8, mesh_show_wireframe=True)
mesh = mesh.subdivide_midpoint(number_of_iterations=1)
print(
f'After subdivision it has {len(mesh.vertices)} vertices and {len(mesh.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh], zoom=0.8, mesh_show_wireframe=True)
The mesh has 8 vertices and 12 triangles

After subdivision it has 26 vertices and 48 triangles

Open3D implements an additional subdivision method based on [Loop1987]. The method is based on a quartic box spline, which generates \(C^2\) continuous limit surfaces everywhere except at extraordinary vertices where they are \(C^1\) continuous. This leads to smoother corners.
[17]:
mesh = o3d.geometry.TriangleMesh.create_sphere()
mesh.compute_vertex_normals()
print(
f'The mesh has {len(mesh.vertices)} vertices and {len(mesh.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh], zoom=0.8, mesh_show_wireframe=True)
mesh = mesh.subdivide_loop(number_of_iterations=2)
print(
f'After subdivision it has {len(mesh.vertices)} vertices and {len(mesh.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh], zoom=0.8, mesh_show_wireframe=True)
The mesh has 762 vertices and 1520 triangles

After subdivision it has 12162 vertices and 24320 triangles

[18]:
mesh = o3dtut.get_knot_mesh()
mesh.compute_vertex_normals()
print(
f'The mesh has {len(mesh.vertices)} vertices and {len(mesh.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh], zoom=0.8, mesh_show_wireframe=True)
mesh = mesh.subdivide_loop(number_of_iterations=1)
print(
f'After subdivision it has {len(mesh.vertices)} vertices and {len(mesh.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh], zoom=0.8, mesh_show_wireframe=True)
The mesh has 1440 vertices and 2880 triangles

After subdivision it has 5760 vertices and 11520 triangles

Mesh simplification¶
Sometimes we want to represent a high-resolution mesh with fewer triangles and vertices, but the low-resolution mesh should still be close to the high-resolution mesh. For this purpose Open3D implements a number of mesh simplification methods.
Vertex clustering¶
The vertex clustering method pools all vertices that fall into a voxel of a given size to a single vertex. The method is implemented in simplify_vertex_clustering and has as parameters voxel_size that defines the size of the voxel grid and contraction that defines how the vertices are pooled. o3d.geometry.SimplificationContraction.Average computes a simple average.
[19]:
mesh_in = o3dtut.get_bunny_mesh()
print(
f'Input mesh has {len(mesh_in.vertices)} vertices and {len(mesh_in.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh_in])
voxel_size = max(mesh_in.get_max_bound() - mesh_in.get_min_bound()) / 32
print(f'voxel_size = {voxel_size:e}')
mesh_smp = mesh_in.simplify_vertex_clustering(
voxel_size=voxel_size,
contraction=o3d.geometry.SimplificationContraction.Average)
print(
f'Simplified mesh has {len(mesh_smp.vertices)} vertices and {len(mesh_smp.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh_smp])
voxel_size = max(mesh_in.get_max_bound() - mesh_in.get_min_bound()) / 16
print(f'voxel_size = {voxel_size:e}')
mesh_smp = mesh_in.simplify_vertex_clustering(
voxel_size=voxel_size,
contraction=o3d.geometry.SimplificationContraction.Average)
print(
f'Simplified mesh has {len(mesh_smp.vertices)} vertices and {len(mesh_smp.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh_smp])
Input mesh has 35947 vertices and 69451 triangles

voxel_size = 4.865594e-03
Simplified mesh has 3222 vertices and 6454 triangles

voxel_size = 9.731187e-03
Simplified mesh has 845 vertices and 1724 triangles

Mesh decimation¶
Another category of mesh simplification methods is mesh decimation that operates in incremental steps. We select a single triangle that minimizes an error metric and removes it. This is repeated until a required number of triangles is achieved. Open3D implements simplify_quadric_decimation that minimizes error quadrics (distances to neighboring planes). The parameter target_number_of_triangles defines the stopping critera of the decimation algorithm.
[20]:
mesh_smp = mesh_in.simplify_quadric_decimation(target_number_of_triangles=6500)
print(
f'Simplified mesh has {len(mesh_smp.vertices)} vertices and {len(mesh_smp.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh_smp])
mesh_smp = mesh_in.simplify_quadric_decimation(target_number_of_triangles=1700)
print(
f'Simplified mesh has {len(mesh_smp.vertices)} vertices and {len(mesh_smp.triangles)} triangles'
)
o3d.visualization.draw_geometries([mesh_smp])
Simplified mesh has 4405 vertices and 6499 triangles

Simplified mesh has 1978 vertices and 1700 triangles

Connected components¶
The result of various reconstruction methods. Open3D implements a connected components algorithm cluster_connected_triangles that assigns each triangle to a cluster of connected triangles. It returns for each triangle the index of the cluster in triangle_clusters, and per cluster the number of triangles in cluster_n_triangles and the surface area of the cluster in cluster_area.
This is useful in for instance RGBD Integration, which is not always a single triangle mesh, but a number of meshes. Some of the smaller parts are due to noise and we most likely want to remove them.
The code below shows the application of cluster_connected_triangles and how it can be used to remove spurious triangles.
[21]:
print("Generate data")
mesh = o3dtut.get_bunny_mesh().subdivide_midpoint(number_of_iterations=2)
vert = np.asarray(mesh.vertices)
min_vert, max_vert = vert.min(axis=0), vert.max(axis=0)
for _ in range(30):
cube = o3d.geometry.TriangleMesh.create_box()
cube.scale(0.005, center=cube.get_center())
cube.translate(
(
np.random.uniform(min_vert[0], max_vert[0]),
np.random.uniform(min_vert[1], max_vert[1]),
np.random.uniform(min_vert[2], max_vert[2]),
),
relative=False,
)
mesh += cube
mesh.compute_vertex_normals()
print("Show input mesh")
o3d.visualization.draw_geometries([mesh])
Generate data
Show input mesh
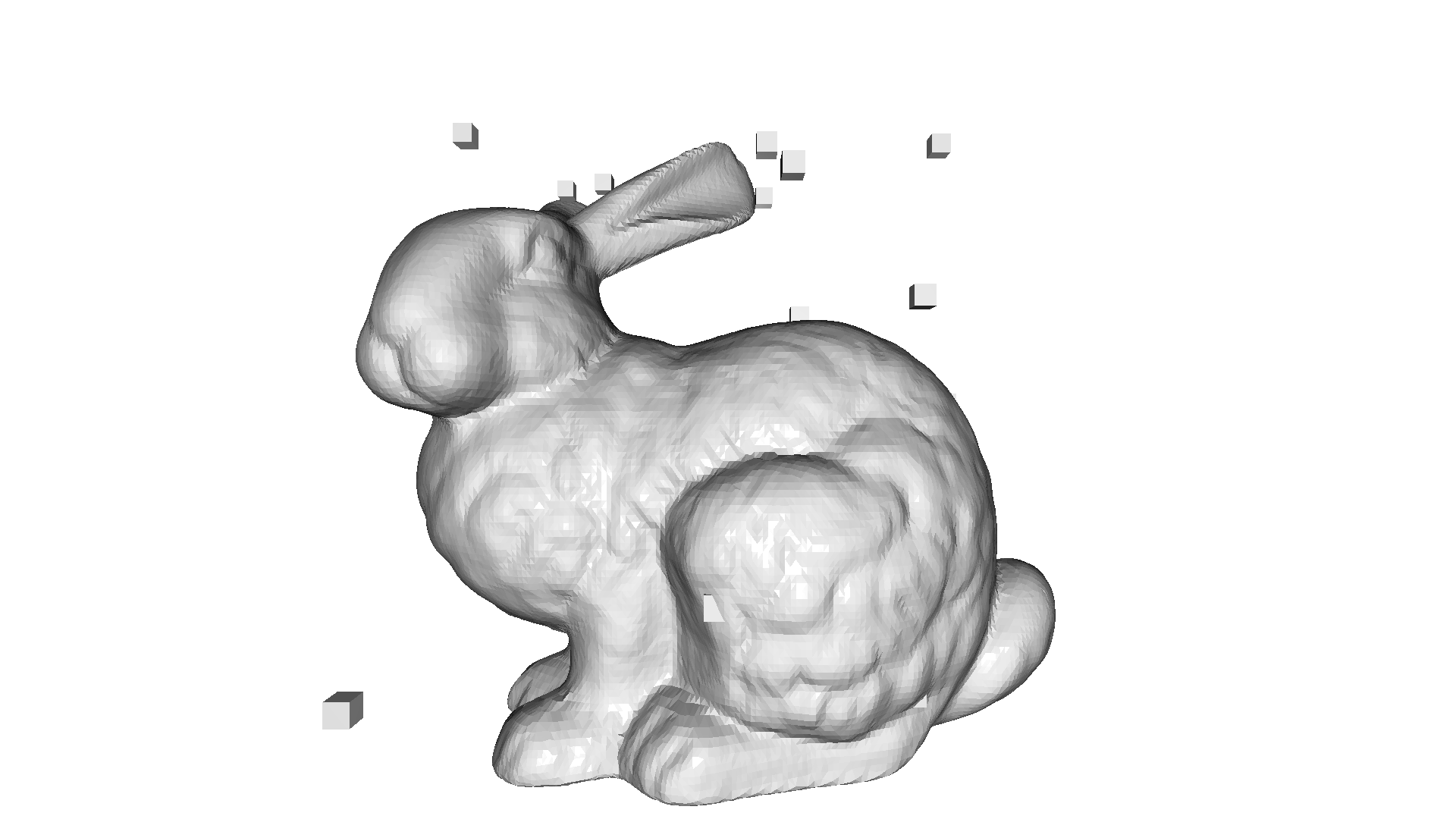
[22]:
print("Cluster connected triangles")
with o3d.utility.VerbosityContextManager(
o3d.utility.VerbosityLevel.Debug) as cm:
triangle_clusters, cluster_n_triangles, cluster_area = (
mesh.cluster_connected_triangles())
triangle_clusters = np.asarray(triangle_clusters)
cluster_n_triangles = np.asarray(cluster_n_triangles)
cluster_area = np.asarray(cluster_area)
Cluster connected triangles
[Open3D DEBUG] [ClusterConnectedTriangles] Compute triangle adjacency
[Open3D DEBUG] [ClusterConnectedTriangles] Done computing triangle adjacency
[Open3D DEBUG] [ClusterConnectedTriangles] Done clustering, #clusters=31
[23]:
print("Show mesh with small clusters removed")
mesh_0 = copy.deepcopy(mesh)
triangles_to_remove = cluster_n_triangles[triangle_clusters] < 100
mesh_0.remove_triangles_by_mask(triangles_to_remove)
o3d.visualization.draw_geometries([mesh_0])
Show mesh with small clusters removed

[24]:
print("Show largest cluster")
mesh_1 = copy.deepcopy(mesh)
largest_cluster_idx = cluster_n_triangles.argmax()
triangles_to_remove = triangle_clusters != largest_cluster_idx
mesh_1.remove_triangles_by_mask(triangles_to_remove)
o3d.visualization.draw_geometries([mesh_1])
Show largest cluster
