Octree

An octree is a tree data structure where each internal node has eight children. Octrees are commonly used for spatial partitioning of 3D point clouds. Non-empty leaf nodes of an octree contain one or more points that fall within the same spatial subdivision. Octrees are a useful description of 3D space and can be used to quickly find nearby points. Open3D has the geometry type Octree that can be used to create, search, and traverse octrees with a user-specified maximum tree depth, max_depth.

From point cloud

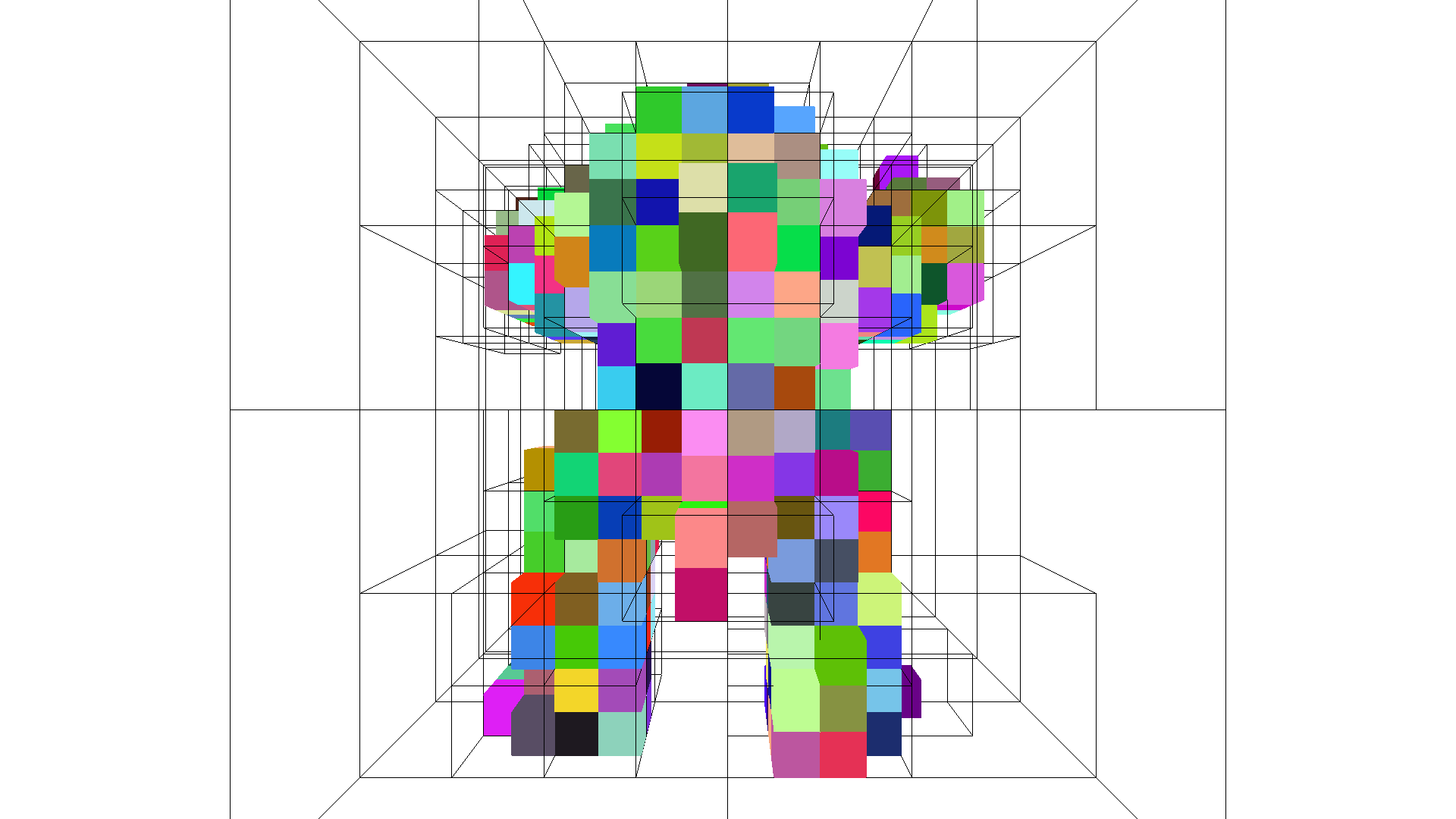
An octree can be constructed from a point cloud using the method convert_from_point_cloud. Each point is inserted into the tree by following the path from the root node to the appropriate leaf node at depth max_depth. As the tree depth increases, internal (and eventually leaf) nodes represents a smaller partition of 3D space.

If the point cloud has color, the the corresponding leaf node takes the color of the last inserted point. The size_expand parameter increases the size of the root octree node so it is slightly bigger than the original point cloud bounds to accommodate all points.

print('input')
N = 2000

armadillo = o3d.data.ArmadilloMesh()
mesh = o3d.io.read_triangle_mesh(armadillo.path)
pcd = mesh.sample_points_poisson_disk(N)
# fit to unit cube
pcd.scale(1 / np.max(pcd.get_max_bound() - pcd.get_min_bound()),
          center=pcd.get_center())
pcd.colors = o3d.utility.Vector3dVector(np.random.uniform(0, 1, size=(N, 3)))
o3d.visualization.draw_geometries([pcd])

print('octree division')
octree = o3d.geometry.Octree(max_depth=4)
octree.convert_from_point_cloud(pcd, size_expand=0.01)
o3d.visualization.draw_geometries([octree])

input
[Open3D WARNING] GLFW Error: Failed to detect any supported platform
[Open3D WARNING] GLFW initialized for headless rendering.

error: XDG_RUNTIME_DIR not set in the environment.

octree division
[Open3D WARNING] GLFW initialized for headless rendering.

From voxel grid

An octree can also be constructed from an Open3D VoxelGrid geometry using the method create_from_voxel_grid. Each voxel of the input VoxelGrid is treated as a point in 3D space with coordinates corresponding to the origin of the voxel. Each leaf node takes the color of its corresponding voxel.

print('voxelization')
voxel_grid = o3d.geometry.VoxelGrid.create_from_point_cloud(pcd,
                                                            voxel_size=0.05)
o3d.visualization.draw_geometries([voxel_grid])

print('octree division')
octree = o3d.geometry.Octree(max_depth=4)
octree.create_from_voxel_grid(voxel_grid)
o3d.visualization.draw_geometries([octree])

voxelization
[Open3D WARNING] GLFW initialized for headless rendering.

octree division
[Open3D WARNING] GLFW initialized for headless rendering.

Additionally, an Octree can be converted to a VoxelGrid with to_voxel_grid.

Traversal

An octree can be traversed which can be useful for searching or processing subsections of 3D geometry. By providing the traverse method with a callback, each time a node (internal or leaf) is visited, additional processing can be performed.

In the following example, an early stopping criterion is used to only process internal/leaf nodes with more than a certain number of points. This early stopping ability can be used to efficiently process spatial regions meeting certain conditions.

def f_traverse(node, node_info):
    early_stop = False

    if isinstance(node, o3d.geometry.OctreeInternalNode):
        if isinstance(node, o3d.geometry.OctreeInternalPointNode):
            n = 0
            for child in node.children:
                if child is not None:
                    n += 1
            print(
                "{}{}: Internal node at depth {} has {} children and {} points ({})"
                .format('    ' * node_info.depth,
                        node_info.child_index, node_info.depth, n,
                        len(node.indices), node_info.origin))

            # we only want to process nodes / spatial regions with enough points
            early_stop = len(node.indices) < 250
    elif isinstance(node, o3d.geometry.OctreeLeafNode):
        if isinstance(node, o3d.geometry.OctreePointColorLeafNode):
            print("{}{}: Leaf node at depth {} has {} points with origin {}".
                  format('    ' * node_info.depth, node_info.child_index,
                         node_info.depth, len(node.indices), node_info.origin))
    else:
        raise NotImplementedError('Node type not recognized!')

    # early stopping: if True, traversal of children of the current node will be skipped
    return early_stop

octree = o3d.geometry.Octree(max_depth=4)
octree.convert_from_point_cloud(pcd, size_expand=0.01)
octree.traverse(f_traverse)

0: Internal node at depth 0 has 8 children and 2000 points ([-2.6581465  31.45477876  1.92536485])
    0: Internal node at depth 1 has 4 children and 54 points ([-2.6581465  31.45477876  1.92536485])
    1: Internal node at depth 1 has 2 children and 41 points ([-2.1531465  31.45477876  1.92536485])
    2: Internal node at depth 1 has 8 children and 408 points ([-2.6581465  31.95977876  1.92536485])
        0: Internal node at depth 2 has 2 children and 6 points ([-2.6581465  31.95977876  1.92536485])
        1: Internal node at depth 2 has 1 children and 5 points ([-2.4056465  31.95977876  1.92536485])
        2: Internal node at depth 2 has 4 children and 43 points ([-2.6581465  32.21227876  1.92536485])
        3: Internal node at depth 2 has 1 children and 5 points ([-2.4056465  32.21227876  1.92536485])
        4: Internal node at depth 2 has 4 children and 54 points ([-2.6581465  31.95977876  2.17786485])
        5: Internal node at depth 2 has 5 children and 92 points ([-2.4056465  31.95977876  2.17786485])
        6: Internal node at depth 2 has 4 children and 78 points ([-2.6581465  32.21227876  2.17786485])
        7: Internal node at depth 2 has 6 children and 125 points ([-2.4056465  32.21227876  2.17786485])
    3: Internal node at depth 1 has 7 children and 369 points ([-2.1531465  31.95977876  1.92536485])
        0: Internal node at depth 2 has 1 children and 4 points ([-2.1531465  31.95977876  1.92536485])
        2: Internal node at depth 2 has 1 children and 6 points ([-2.1531465  32.21227876  1.92536485])
        3: Internal node at depth 2 has 3 children and 11 points ([-1.9006465  32.21227876  1.92536485])
        4: Internal node at depth 2 has 4 children and 80 points ([-2.1531465  31.95977876  2.17786485])
        5: Internal node at depth 2 has 4 children and 48 points ([-1.9006465  31.95977876  2.17786485])
        6: Internal node at depth 2 has 6 children and 113 points ([-2.1531465  32.21227876  2.17786485])
        7: Internal node at depth 2 has 6 children and 107 points ([-1.9006465  32.21227876  2.17786485])
    4: Internal node at depth 1 has 5 children and 350 points ([-2.6581465  31.45477876  2.43036485])
        0: Internal node at depth 2 has 4 children and 62 points ([-2.6581465  31.45477876  2.43036485])
        1: Internal node at depth 2 has 4 children and 100 points ([-2.4056465  31.45477876  2.43036485])
        2: Internal node at depth 2 has 2 children and 20 points ([-2.6581465  31.70727876  2.43036485])
        3: Internal node at depth 2 has 8 children and 146 points ([-2.4056465  31.70727876  2.43036485])
        7: Internal node at depth 2 has 1 children and 22 points ([-2.4056465  31.70727876  2.68286485])
    5: Internal node at depth 1 has 4 children and 318 points ([-2.1531465  31.45477876  2.43036485])
        0: Internal node at depth 2 has 8 children and 169 points ([-2.1531465  31.45477876  2.43036485])
        1: Internal node at depth 2 has 1 children and 1 points ([-1.9006465  31.45477876  2.43036485])
        2: Internal node at depth 2 has 8 children and 146 points ([-2.1531465  31.70727876  2.43036485])
        6: Internal node at depth 2 has 1 children and 2 points ([-2.1531465  31.70727876  2.68286485])
    6: Internal node at depth 1 has 6 children and 241 points ([-2.6581465  31.95977876  2.43036485])
    7: Internal node at depth 1 has 6 children and 219 points ([-2.1531465  31.95977876  2.43036485])

Find leaf node containing point

Using the above traversal mechanism, an octree can be quickly searched for the leaf node that contains a given point. This functionality is provided via the locate_leaf_node method.

octree.locate_leaf_node(pcd.points[0])

(OctreePointColorLeafNode with color [0.0848246, 0.594436, 0.105971] containing 6 points.,
 OctreeNodeInfo with origin [-2.09002, 32.2754, 2.30411], size 0.063125, depth 4, child_index 3)