Point cloud#
This tutorial demonstrates basic usage of a point cloud.
Visualize point cloud#
The first part of the tutorial reads a point cloud and visualizes it.
[2]:
print("Load a ply point cloud, print it, and render it")
ply_point_cloud = o3d.data.PLYPointCloud()
pcd = o3d.io.read_point_cloud(ply_point_cloud.path)
print(pcd)
print(np.asarray(pcd.points))
o3d.visualization.draw_geometries([pcd],
zoom=0.3412,
front=[0.4257, -0.2125, -0.8795],
lookat=[2.6172, 2.0475, 1.532],
up=[-0.0694, -0.9768, 0.2024])
Load a ply point cloud, print it, and render it
PointCloud with 196133 points.
[[0.65234375 0.84686458 2.37890625]
[0.65234375 0.83984375 2.38430572]
[0.66737998 0.83984375 2.37890625]
...
[2.00839925 2.39453125 1.88671875]
[2.00390625 2.39488506 1.88671875]
[2.00390625 2.39453125 1.88793314]]
read_point_cloud reads a point cloud from a file. It tries to decode the file based on the extension name. For a list of supported file types, refer to File IO.
draw_geometries visualizes the point cloud. Use a mouse/trackpad to see the geometry from different view points.
It looks like a dense surface, but it is actually a point cloud rendered as surfels. The GUI supports various keyboard functions. For instance, the - key reduces the size of the points (surfels).
Note:
Press the H key to print out a complete list of keyboard instructions for the GUI. For more information of the visualization GUI, refer to Visualization and Customized visualization.
Note:
On macOS, the GUI window may not receive keyboard events. In this case, try to launch Python with pythonw instead of python.
Voxel downsampling#
Voxel downsampling uses a regular voxel grid to create a uniformly downsampled point cloud from an input point cloud. It is often used as a pre-processing step for many point cloud processing tasks. The algorithm operates in two steps:
Points are bucketed into voxels.
Each occupied voxel generates exactly one point by averaging all points inside.
[3]:
print("Downsample the point cloud with a voxel of 0.05")
downpcd = pcd.voxel_down_sample(voxel_size=0.05)
o3d.visualization.draw_geometries([downpcd],
zoom=0.3412,
front=[0.4257, -0.2125, -0.8795],
lookat=[2.6172, 2.0475, 1.532],
up=[-0.0694, -0.9768, 0.2024])
Downsample the point cloud with a voxel of 0.05
Vertex normal estimation#
Another basic operation for point cloud is point normal estimation. Press N to see point normals. The keys - and + can be used to control the length of the normal.
[4]:
print("Recompute the normal of the downsampled point cloud")
downpcd.estimate_normals(
search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
o3d.visualization.draw_geometries([downpcd],
zoom=0.3412,
front=[0.4257, -0.2125, -0.8795],
lookat=[2.6172, 2.0475, 1.532],
up=[-0.0694, -0.9768, 0.2024],
point_show_normal=True)
Recompute the normal of the downsampled point cloud
estimate_normals computes the normal for every point. The function finds adjacent points and calculates the principal axis of the adjacent points using covariance analysis.
The function takes an instance of KDTreeSearchParamHybrid class as an argument. The two key arguments radius = 0.1 and max_nn = 30 specifies search radius and maximum nearest neighbor. It has 10cm of search radius, and only considers up to 30 neighbors to save computation time.
Note:
The covariance analysis algorithm produces two opposite directions as normal candidates. Without knowing the global structure of the geometry, both can be correct. This is known as the normal orientation problem. Open3D tries to orient the normal to align with the original normal if it exists. Otherwise, Open3D does a random guess. Further orientation functions such as orient_normals_to_align_with_direction and orient_normals_towards_camera_location need to be called if the orientation
is a concern.
Access estimated vertex normal#
Estimated normal vectors can be retrieved from the normals variable of downpcd.
[5]:
print("Print a normal vector of the 0th point")
print(downpcd.normals[0])
Print a normal vector of the 0th point
[-0.27566603 -0.89197839 -0.35830543]
To check out other variables, please use help(downpcd). Normal vectors can be transformed as a numpy array using np.asarray.
[6]:
print("Print the normal vectors of the first 10 points")
print(np.asarray(downpcd.normals)[:10, :])
Print the normal vectors of the first 10 points
[[-0.27566603 -0.89197839 -0.35830543]
[-0.04230441 -0.99410664 -0.09981149]
[-0.00399871 -0.99965423 -0.02598917]
[-0.93768261 -0.07378998 0.3395679 ]
[-0.43476205 -0.62438493 -0.64894177]
[-0.09739809 -0.9928602 -0.06886388]
[-0.27498453 -0.67317361 -0.68645524]
[-0.11728718 -0.95516445 -0.27185399]
[-0.00816546 -0.99965616 -0.02491762]
[-0.11067463 -0.99205156 -0.05987351]]
Check Working with NumPy for more examples regarding numpy arrays.
Crop point cloud#
[7]:
print("Load a polygon volume and use it to crop the original point cloud")
demo_crop_data = o3d.data.DemoCropPointCloud()
pcd = o3d.io.read_point_cloud(demo_crop_data.point_cloud_path)
vol = o3d.visualization.read_selection_polygon_volume(demo_crop_data.cropped_json_path)
chair = vol.crop_point_cloud(pcd)
o3d.visualization.draw_geometries([chair],
zoom=0.7,
front=[0.5439, -0.2333, -0.8060],
lookat=[2.4615, 2.1331, 1.338],
up=[-0.1781, -0.9708, 0.1608])
Load a polygon volume and use it to crop the original point cloud
read_selection_polygon_volume reads a json file that specifies polygon selection area. vol.crop_point_cloud(pcd) filters out points. Only the chair remains.
Paint point cloud#
[8]:
print("Paint chair")
chair.paint_uniform_color([1, 0.706, 0])
o3d.visualization.draw_geometries([chair],
zoom=0.7,
front=[0.5439, -0.2333, -0.8060],
lookat=[2.4615, 2.1331, 1.338],
up=[-0.1781, -0.9708, 0.1608])
Paint chair
paint_uniform_color paints all the points to a uniform color. The color is in RGB space, [0, 1] range.
Point cloud distance#
Open3D provides the method compute_point_cloud_distance to compute the distance from a source point cloud to a target point cloud. I.e., it computes for each point in the source point cloud the distance to the closest point in the target point cloud.
In the example below we use the function to compute the difference between two point clouds. Note that this method could also be used to compute the Chamfer distance between two point clouds.
[9]:
# Load data
demo_crop_data = o3d.data.DemoCropPointCloud()
pcd = o3d.io.read_point_cloud(demo_crop_data.point_cloud_path)
vol = o3d.visualization.read_selection_polygon_volume(demo_crop_data.cropped_json_path)
chair = vol.crop_point_cloud(pcd)
dists = pcd.compute_point_cloud_distance(chair)
dists = np.asarray(dists)
ind = np.where(dists > 0.01)[0]
pcd_without_chair = pcd.select_by_index(ind)
o3d.visualization.draw_geometries([pcd_without_chair],
zoom=0.3412,
front=[0.4257, -0.2125, -0.8795],
lookat=[2.6172, 2.0475, 1.532],
up=[-0.0694, -0.9768, 0.2024])
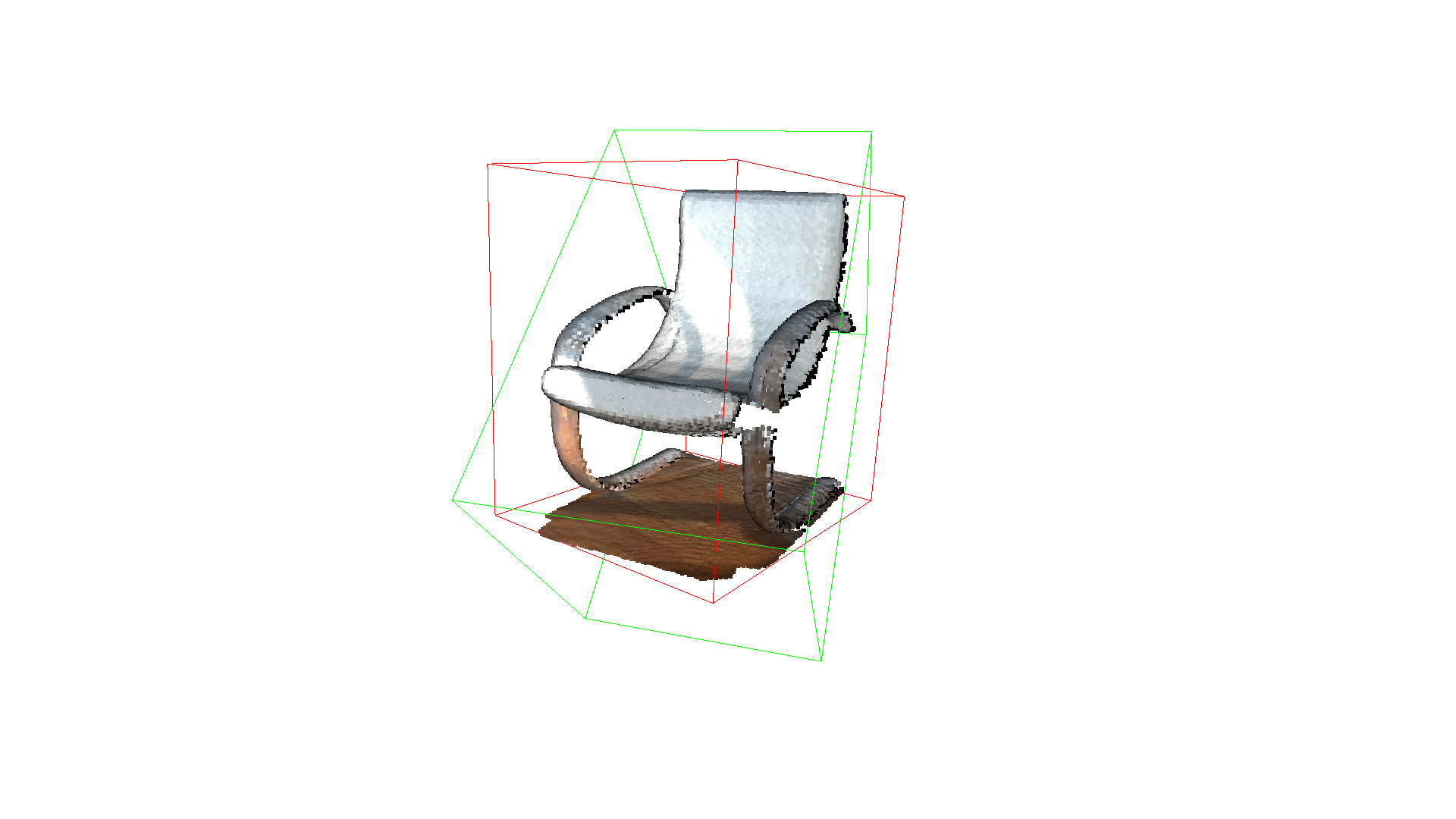
Bounding volumes#
The PointCloud geometry type has bounding volumes as all other geometry types in Open3D. Currently, Open3D implements an AxisAlignedBoundingBox and an OrientedBoundingBox that can also be used to crop the geometry.
[10]:
aabb = chair.get_axis_aligned_bounding_box()
aabb.color = (1, 0, 0)
obb = chair.get_oriented_bounding_box()
obb.color = (0, 1, 0)
o3d.visualization.draw_geometries([chair, aabb, obb],
zoom=0.7,
front=[0.5439, -0.2333, -0.8060],
lookat=[2.4615, 2.1331, 1.338],
up=[-0.1781, -0.9708, 0.1608])
Convex hull#
The convex hull of a point cloud is the smallest convex set that contains all points. Open3D contains the method compute_convex_hull that computes the convex hull of a point cloud. The implementation is based on Qhull.
In the example code below we first sample a point cloud from a mesh and compute the convex hull that is returned as a triangle mesh. Then, we visualize the convex hull as a red LineSet.
[11]:
bunny = o3d.data.BunnyMesh()
mesh = o3d.io.read_triangle_mesh(bunny.path)
mesh.compute_vertex_normals()
pcl = mesh.sample_points_poisson_disk(number_of_points=2000)
hull, _ = pcl.compute_convex_hull()
hull_ls = o3d.geometry.LineSet.create_from_triangle_mesh(hull)
hull_ls.paint_uniform_color((1, 0, 0))
o3d.visualization.draw_geometries([pcl, hull_ls])
DBSCAN clustering#
Given a point cloud from e.g. a depth sensor we want to group local point cloud clusters together. For this purpose, we can use clustering algorithms. Open3D implements DBSCAN [Ester1996] that is a density based clustering algorithm. The algorithm is implemented in cluster_dbscan and requires two parameters: eps defines the distance to neighbors in a cluster and min_points defines the minimum number of points required to form a cluster. The function
returns labels, where the label -1 indicates noise.
[12]:
ply_point_cloud = o3d.data.PLYPointCloud()
pcd = o3d.io.read_point_cloud(ply_point_cloud.path)
with o3d.utility.VerbosityContextManager(
o3d.utility.VerbosityLevel.Debug) as cm:
labels = np.array(
pcd.cluster_dbscan(eps=0.02, min_points=10, print_progress=True))
max_label = labels.max()
print(f"point cloud has {max_label + 1} clusters")
colors = plt.get_cmap("tab20")(labels / (max_label if max_label > 0 else 1))
colors[labels < 0] = 0
pcd.colors = o3d.utility.Vector3dVector(colors[:, :3])
o3d.visualization.draw_geometries([pcd],
zoom=0.455,
front=[-0.4999, -0.1659, -0.8499],
lookat=[2.1813, 2.0619, 2.0999],
up=[0.1204, -0.9852, 0.1215])
[Open3D DEBUG] Precompute neighbors.
[Open3D DEBUG] Done Precompute neighbors.
[Open3D DEBUG] Compute Clusters
Precompute neighbors.[========================================] 100%
[Open3D DEBUG] Done Compute Clusters: 10
point cloud has 10 clusters
Note:
This algorithm precomputes all neighbors in the epsilon radius for all points. This can require a lot of memory if the chosen epsilon is too large.
Plane segmentation#
Open3D also supports segmententation of geometric primitives from point clouds using RANSAC. To find the plane with the largest support in the point cloud, we can use segment_plane. The method has three arguments: distance_threshold defines the maximum distance a point can have to an estimated plane to be considered an inlier, ransac_n defines the number of points that are randomly sampled to estimate a plane, and num_iterations defines how often a random plane is sampled and
verified. The function then returns the plane as \((a,b,c,d)\) such that for each point \((x,y,z)\) on the plane we have \(ax + by + cz + d = 0\). The function further returns a list of indices of the inlier points.
[13]:
pcd_point_cloud = o3d.data.PCDPointCloud()
pcd = o3d.io.read_point_cloud(pcd_point_cloud.path)
plane_model, inliers = pcd.segment_plane(distance_threshold=0.01,
ransac_n=3,
num_iterations=1000)
[a, b, c, d] = plane_model
print(f"Plane equation: {a:.2f}x + {b:.2f}y + {c:.2f}z + {d:.2f} = 0")
inlier_cloud = pcd.select_by_index(inliers)
inlier_cloud.paint_uniform_color([1.0, 0, 0])
outlier_cloud = pcd.select_by_index(inliers, invert=True)
o3d.visualization.draw_geometries([inlier_cloud, outlier_cloud],
zoom=0.8,
front=[-0.4999, -0.1659, -0.8499],
lookat=[2.1813, 2.0619, 2.0999],
up=[0.1204, -0.9852, 0.1215])
Plane equation: -0.06x + -0.10y + 0.99z + -1.06 = 0
Planar patch detection#
In addition to finding the single plane with the largest support, Open3D includes an algorithm which uses a robust statistics-based approach for planar patch detection [ArujoAndOliveira2020]. This algorithm first subdivides the point cloud into smaller chunks (using an octree), then attempts to fit a plane to each chunk. If the plane passes a robust planarity test, then it is accepted. A plane is fitted to a subset of points by taking the median point position and the median point normal and estimating a plane \(ax + by + cz + d = 0\). The robust planarity check consists of two main components. First, the distribution of angles between each point normal and the fitted plane normal is found. If the spread of this distribution is too high (i.e., there is too much variance amongst all of the associated point normals), then the plane is rejected. Second, the distribution of the distances from the fitted plane to each point is computed. If the spread of this distribution is too high, as measured using a coplanarity metric (see Fig. 4 of [ArujoAndOliveira2020]), then the plane is rejected. After an initial set of planes are found, an iterative procedure is used to grow and merge planes into a smaller, stable set of planes. These planes can then be bounded using the 2D convex hull of their associated point sets and planar patches are extracted.
To find a list of planar patches in a point cloud, we can use detect_planar_patches. This method can take six arguments: normal_variance_threshold_deg controls the amount of variance allowed amongst the point normals and takes \(60^\circ\) as its default. Smaller values tends to result in fewer, higher quality planes. coplanarity_deg controls the allowed distribution of point distances from the plane and takes \(75^\circ\) as its default. Larger values encourage a tighter
distribution of points around the fitted plane. outlier_ratio sets the maximum allowable outlier ratio in a fitted planes associated set of points before being rejected and has the default value of 0.75. min_plane_edge_length is used to reject false positives—a planar patch’s largest edge much be greater than this value to be considered a true planar patch. If left at 0, the algorithm defaults to using a value of 1% of the point clouds largest dimension. min_num_points
determines how deep the associated octree becomes and how many points must be present when attempting to fit a plane. If left at 0, the algorithm defaults to 0.1% of the number of points in the point cloud. search_param is an instance of geometry::KDTreeSearchParam and defaults to geometry::KDTreeSearchParamKNN. The k nearest neighbors to each point are used when growing and merging planes. Larger values of k tend to produce higher quality patches at the expense of
computation. This function then returns a list of detected planar patches, represented as geometry::OrientedBoundingBox objects, with the third column (i.e., \(z\)) of R indicating the planar patch normal vector. The extent in the \(z\) direction is non-zero so that the OrientedBoundingBox contains the points that contribute to the plane detection. The planar patches can be visualized using the geometry::TriangleMesh::CreateFromOrientedBoundingBox factory function, using the
scale parameter to “flatten” the bounding box along the normal, i.e., CreateFromOrientedBoundingBox(obox, scale=[1, 1, 0.0001]).
[14]:
dataset = o3d.data.PCDPointCloud()
pcd = o3d.io.read_point_cloud(dataset.path)
assert (pcd.has_normals())
# using all defaults
oboxes = pcd.detect_planar_patches(
normal_variance_threshold_deg=60,
coplanarity_deg=75,
outlier_ratio=0.75,
min_plane_edge_length=0,
min_num_points=0,
search_param=o3d.geometry.KDTreeSearchParamKNN(knn=30))
print("Detected {} patches".format(len(oboxes)))
geometries = []
for obox in oboxes:
mesh = o3d.geometry.TriangleMesh.create_from_oriented_bounding_box(obox, scale=[1, 1, 0.0001])
mesh.paint_uniform_color(obox.color)
geometries.append(mesh)
geometries.append(obox)
geometries.append(pcd)
o3d.visualization.draw_geometries(geometries,
zoom=0.62,
front=[0.4361, -0.2632, -0.8605],
lookat=[2.4947, 1.7728, 1.5541],
up=[-0.1726, -0.9630, 0.2071])
Detected 10 patches
Hidden point removal#
Imagine you want to render a point cloud from a given view point, but points from the background leak into the foreground because they are not occluded by other points. For this purpose we can apply a hidden point removal algorithm. In Open3D the method by [Katz2007] is implemented that approximates the visibility of a point cloud from a given view without surface reconstruction or normal estimation.
[15]:
print("Convert mesh to a point cloud and estimate dimensions")
armadillo = o3d.data.ArmadilloMesh()
mesh = o3d.io.read_triangle_mesh(armadillo.path)
mesh.compute_vertex_normals()
pcd = mesh.sample_points_poisson_disk(5000)
diameter = np.linalg.norm(
np.asarray(pcd.get_max_bound()) - np.asarray(pcd.get_min_bound()))
o3d.visualization.draw_geometries([pcd])
Convert mesh to a point cloud and estimate dimensions
[16]:
print("Define parameters used for hidden_point_removal")
camera = [0, 0, diameter]
radius = diameter * 100
print("Get all points that are visible from given view point")
_, pt_map = pcd.hidden_point_removal(camera, radius)
print("Visualize result")
pcd = pcd.select_by_index(pt_map)
o3d.visualization.draw_geometries([pcd])
Define parameters used for hidden_point_removal
Get all points that are visible from given view point
Visualize result
